Face Coordinates : Developer

In This Topic

When doing machining, particularly when donor-acceptor situations are being handled, it is important to understand face coordinates. Typically machining is specified imagining a 2D surface and defining the routing and drilling that takes place on that surface. The machining is defined in "face coordinates". This means that the xy-plane is the face itself, and z is the perpendicular direction to that face.

In order to fully specify face coordinates for any face, you need to know where the origin is on the face (x=0 and y=0, z=0 is always on the face). You should also know the "up" or positive z direction, also called the "normal" direction.

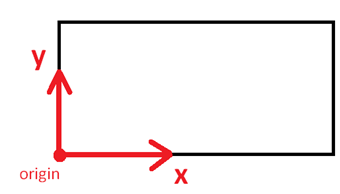
In simple situations, the face coordinates are the "obvious" ones. For example, looking down in plan view at the top face of a section, we see a rectangle, and the origin is the bottom left corner:

In this case the z-axis is the "up" direction. This means that we will need negative values of z to machine into the face. In more general cases, the z-axis is always determined by using the "right hand rule". If you hold your right hand at the origin, and point your thumb along the x-axis and your first finger along the y-axis, then form a right angled shape as shown below, the second finger will point along the z-axis:

Vertical Faces

When we are looking at vertical faces, the situation is like this. Here we are looking at a section which is at the left end of the nominal box, and we have shaded its right face.

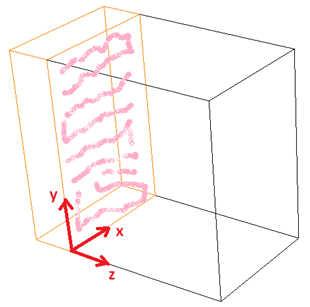
Looking at the right face, the bottom left corner is as shown with x- y- and z-axes marked.

Sections Within Faces

The situation is similar if this section is not in the nominal box, but is constructed by putting it in the left face of the nominal box. We do that like this, (container= means use the nominal cabinet box for a container):

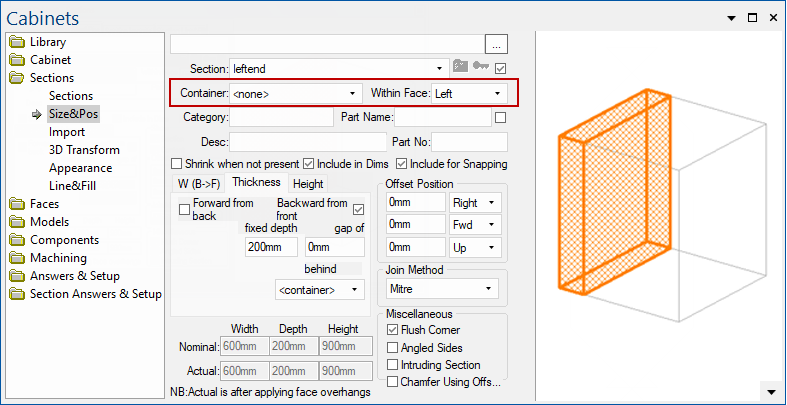
In this case, the shaded face of our earlier diagram is actually the "back face" of this section because we are looking at the left face of the nominal box as a container. However, once we are on this back face, it still has its origin at the lower left corner with x y and z-axes as shown above.

Bottom Faces

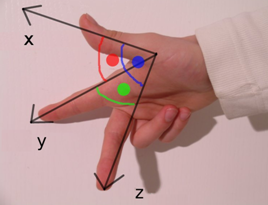
With bottom faces, defining the origin as the "bottom left corner when looking at the face" leaves some ambiguity. To look at the face we have to lie under the cabinet and look up. Now it depends whether we crawl under head first or feet first. In our coordinate system definitions, we have adopted the "AutoCad arbitrary axis algorithm" which resolves this ambiguity, and effectively determines that we must crawl under head first.

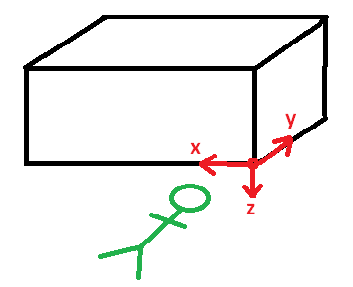
So for the bottom face of a simple section like the one above, we crawl under head first and look upwards at the face, observing the corner marked in red above as our "bottom left" corner, which is therefore the face origin.

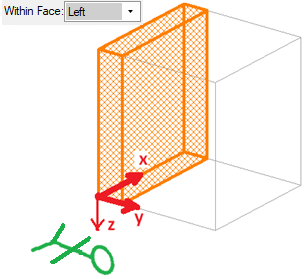
The direction that we crawl is always from the front of the section towards the back. This means that if the section is "within a face" we have to crawl under from that face. So for example, when this section is within the left face of the nominal box, the origin corner is now different:

Face Info Button

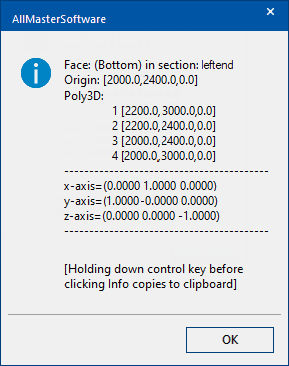
We can use the face "Info" button to check the origin, normal and vertices of a face in world coordinates:

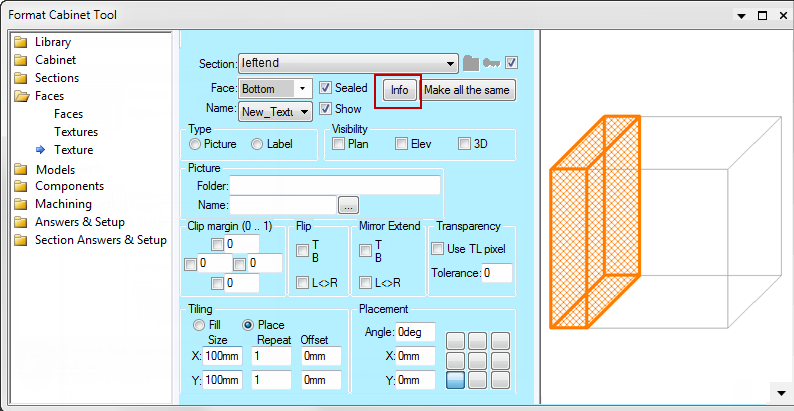
Notice we have selected the bottom face in the dropdown above the Info button, and in this example, the section is within the left face of the nominal box still. So pressing the info button gives this information. You can verify the axis directions are the same as those in the previous section.

When looking at world coordinates, as above, it makes things easier if you ensure the cabinet is not rotated on the drawing page. If you move the cabinet to another position in the drawing or rotate it, this makes no difference to the earlier discussion provided the cabinet is always viewed from its "main front" when determining what is the left end or right end etc. However, world coordinates will of course be altered, so be careful, particularly when trying to interpret the meaning of an axis direction in the face info dialog.

Also, when comparing face info for various different faces, you can use the clipboard to copy the info for each face into another document in Notepad or any other editor. The information on the current face will be placed onto the clipboard if you hold down the "Control" key when clicking on the Info button. In this case, the dialog still appears, but its contents will be copied to the clipboard also. So you can leave Notepad open and switch back and forth pasting the information for each face of interest, using control+V or paste via the editor menus in the usual way.